Unidimensional curve fitting in python
This post is about using scipy.optimize.curve_fit to solve a non-linear least square problem. The documentation for the method can be found here.
Exact model
Suppose one has a function of arbitrary complexity whose expression is known in advance. How easy is it to find the correct parameters ?
After playing with different kinds of four-parameter functions, I stumbled upon the following family:
$$ f_\theta (x) = \dfrac{6\cdot\theta_0^2 + 11\cdot\theta_0\theta_1 \cdot x}{5 + 5(x – \theta_2 )^{2}(x – \theta_2 )^{2 \theta_3}} \sin(x – \theta_1)$$
Three functions from this family, after $y$-axis normalization, are plotted below on a uniform grid:

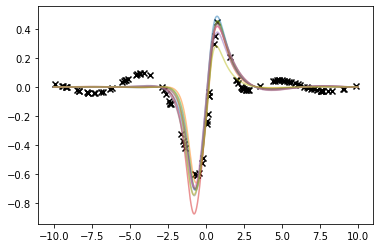
The first function's parameters, as estimated by the curve_fit method by randomly sampling $n=100$ points from the original data with numpy seed 12321. The parameter initialisation is $[0.5, 0.5, 0.5, 0.5]$ which results in the fit
| Parameter | Estimate | Standard Error |
|---|---|---|
| $\theta_0$ | -1.9167 | 0.0199 |
| $\theta_1$ | -0.0981 | 0.0105 |
| $\theta_2$ | -2.6755 | 0.0087 |
| $\theta_3$ | 1.0832 | 0.0596 |
Where all results were truncated to the fourth decimal place. Let's visualize our result:

The fit is perfect, however the parameters are not. This is not an issue for our purposes. However the fit quality highly depends on the points' locations. By changing the seed and fitting a new curve, one obtains the less pleasant fit illustrated below:

This is only a sample size issue. By setting $n = 200$ and running the process again, we obtain the fit

Our second function is much more robust to the training set variations:
The third function's fits for different seeds can be seen below:
