#datastructures #algorithmns #devstudy #BigONotation #timecomplexity #spacecomplexity

Time Complexity: Time taken to run as a function of the length of the input

• number of operations it takes to complete for length Input
• find the WORST CASE scenario > drop the non-dominant terms

Not the most useful chart but that pastel-tone charcoal = yes

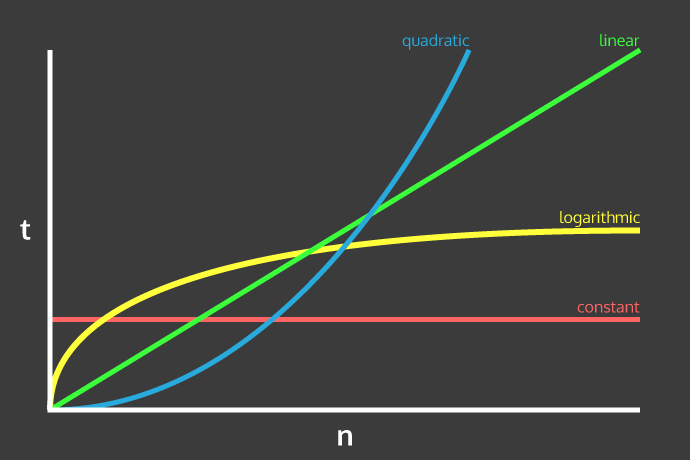
Better chart but less aesthetic:

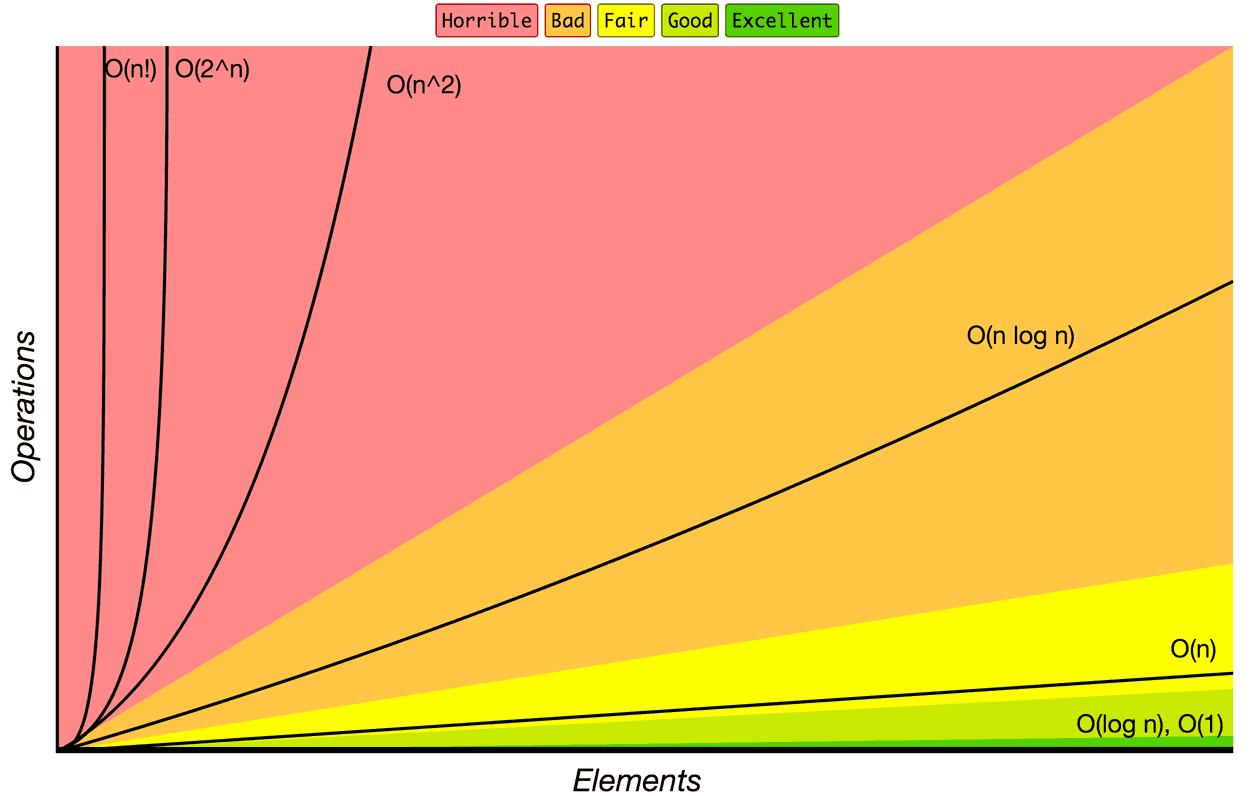
From Fastest to Slowest:

O(1) time: One Operation

• takes a constant amount of time even with more input
• ex: mathematical calculation of sum: s = n(a+1)/2 as opposed iterative calculation which is O(n) linear bc for every additional input value, the rate of growth re: time scales proportionally.

Examples

• accessing Array Index
• Inserting a node in Linked List
• Pushing and Popping on Stack
• Insertion and Removal from Queue
• Finding out the parent or left/right child of a node in a tree stored in Array
• Jumping to Next/Previous element in Doubly Linked List

O(log n) time: Recursion?

Examples

• Binary Search
• Finding largest/smallest number in a binary search tree
• Certain Divide and Conquer Algorithms based on Linear functionality
• Calculating Fibonacci Numbers – Best Method premise = NOT using the complete data, and reducing the problem size with every iteration

O(n) time: Linear, i.e. Brute Force, Noob ones that I write bc my brain is stuck on iteration

Examples

• Traversing an array
• Traversing a linked list
• Linear Search
• Deletion of a specific element in a Linked List (Not sorted)
• Comparing two strings
• Checking for Palindrome
• Counting/Bucket Sort and here too you can find a million more such examples....

O(n*log n) time: linear time complexity multiplied by log n

• factor of log n is introduced by bringing into consideration Divide and Conquer.
• some of the most optimized and frequently used

Examples

• Merge Sort (recursive)
• Heap Sort
• Quick Sort
• Certain Divide and Conquer Algorithms based on optimizing O(n^2) algorithms

O(n^2) time: Quadratic.

• nested loops bc each loop is performing n iterations so n*n
• less efficient algorithms if their O(n*logn) counterparts are present??
• general application may be Brute Force here

Examples

• Bubble Sort :'(
• Insertion Sort
• Selection Sort
• Traversing a simple 2D array

---

Space Complexity: The space an algo needs to run

• sorting algorithmns need at least O(n) space to save the list of length n that they have to sort but can often work in place meaning that it needs no additional space
• number representation can be saved in either (1) binary (or any other base equal or less than 2) so this needs O(log n) space bc n = 2^logn; or (2) as a sum of n so you need O(n) space bc you need to save each n

O(1) space: In-place

• a function that counts the elements of an array: don't need to allocate or copy new data even if the array is large, the counter is the same var

O(log n) space:

Examples

• Binary Search
• Finding largest/smallest number in a binary search tree
• Certain Divide and Conquer Algorithms based on Linear functionality
• Calculating Fibonacci Numbers – Best Method premise = NOT using the complete data, and reducing the problem size with every iteration

O(n) space:

• everytime we make a new function call = new stack frame
  
• recursion: if n = 100, then O(n)