Having reviewed a pile of epidemiological models, and worked on a detailed one myself, it seems long overdue to write a Small Sims post about epidemiological modelling.

The Flu And Coronavirus Simulator we worked on is a bit too extensive to cover in Small Sims, so instead I'll focus on a much simpler model: the so-called SIR model. Here SIR stands for Susceptible, Infectious and Recovered.

Although a lot of advanced articles cover these models, the SIR model itself is actually remarkably simple. As you will find below, we need a lot less code here than for many other Small Sims installments :).

Our platform of choice today is repl.it, where you can create simple Python code fragments and run them.

Without further ado, let's get started!

Setting the scene

First we need to import a few libraries so we can plot stuff:

import matplotlib.pyplot as plt

import matplotlib as mpl

mpl.use('Agg')

Next, we create our population. 998 people are healthy:

S = [998]

Two people are ill and infectious:

I = [2]

And nobody has recovered (yet):

R = [0]

The following variable, beta, indicates the speed that the disease will spread. I picked 0.3, just so that you get a nice-looking graph over 100 time steps:

beta = 0.3

And gamma is the chance of an ill person to recover. A gamma of 0.12 indicates that a person has ill for 1/0.12=8.33 days on average:

gamma = 0.12

Adding the steps

Now the magic is of course not in this starting state, but in how you progress from one state to the next! We do this using a step function:

def Step():

Here, the number of newly infectious people (new_I) is equal to the number of people currently susceptible (S[-1]) times the number of currently infectious (I[-1]), times beta and divided by the total population size (1000).

new_I = beta*S[-1]*I[-1]/1000

Meanwhile, the number of newly recovered people is the number of currently infectious people times gamma:

new_R = gamma*I[-1]

We then subtract the newly infectious people from the susceptible population (allowing for fractions, btw ;)):

S.append(S[-1] - new_I)

and add them to the number of infectious people. In turn, we subtract the number of newly recovered people from the infectious population:

I.append(I[-1] - new_R + new_I)

...and add those to the recovered population!

R.append(R[-1] + new_R)

Five lines: that's literally all the logic we need for a basic model!

Generating the curve

Last task is of course to run the simulation and generate the graph. You can do this as follows:

First print the initial state as a reference:

print(S[-1],I[-1],R[-1])

Next, run the simulation for a hundred steps, and print the three populations after every step:

for i in range(0,100):

Step()

print(S[-1],I[-1],R[-1])

And finally, let's make ourselves a simple plot and write it to a png file!

fig, ax = plt.subplots()

ax.plot(S, label="Susceptible")

ax.plot(I, label="Infectious")

ax.plot(R, label="Recovered")

ax.grid()

ax.legend()

fig.savefig("SIR.png")

When you run this code, and then open SIR.png, you'll see something like this:

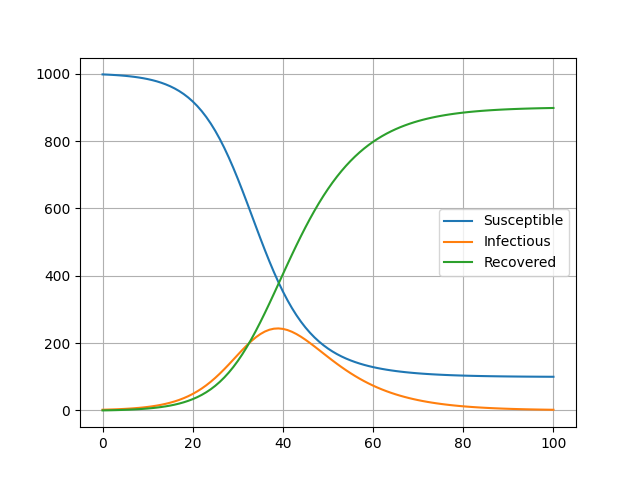
Here you can see the time in days on the x axis, and the number of people in each category on the y axis!

Closing thoughts

And that's all we need really! You can find the Repl.it just below, which allows you to run the thing straight from your browser and double-check the code. Feel free to have a play with the code, and I particularly recommend playing around with the beta values, the gamma values, and the size of the initial population :).

Oh, and if you're keen to check out the other installments of Small Sims, please have a look at the index here.

And for subscribers, I am going the full stretch today by extending the SIR into SEIRD :).

Two things happened this week:

• The journal paper about our local Flu And Coronavirus Simulator got submitted. You can find a pre-print of it here.
• I did yet another review of a Covid-19 model, but this time specifically on behalf of the Conversation, which you can find here. The model in question is quite different to ones I reviewed previously, as it attempts to isolate the causes of Covid-19 using a technique called Bayesian inference.

I might elaborate on both of them a bit more about a later stage, but I just wanted to sign-post them for you all today :).

I also got a few questions about both along the way, and thought I'd use this blog post to summarize the answers for everyone's interest. I will be sure to update these post with new answers whenever I get new questions about these topics :).

About the simulation paper

“Does your model treat each burough as a closed system? That is, does it assume that all residents will stay within the borders, and no non residents will enter?”

- Yes, the model is a closed system, but it is possible to put in a background transmission rate to reflect infections coming from outside.

“The line graphs for each scenario looked very similar between buroughs. Is that indeed the case?”

- There are clear differences, but in North West London the precise differences are indeed not enormous. When you look closely, you can see important differences in the height of the initial peak though, and when a second, slower wave is expected to peak.

“Finally, have you looked at applying the model anywhere else? If I understand the toolkit, it should be easy to apply to other cities?”

- We are already trying out the model on 4 other boroughs in London, and we are preparing for the code to be reused in other cities. The code can be re-used for any local region, except for ones where the necessary OpenStreetMap data is missing or when a region is too large to simulate (more than ~1M household). If a region is too large, it is possible to split it into multiple simulations though. Also, we hope to develop a more efficient parallel version that can cope with larger regions.

“Is there any kind of “feature selection” in your model? That is, of the social gathering spots you looked at, can you see which geographical features make a borough especially vulnerable?”

- The feature selection is relevant actually, because every spot is different. Its location determines which households go there, and the number of square meters can affect how likely the infection is to spread there.

“Do such models [like FACS] give possible answers to some of the questions why some events have been shown to be spreading events, and others haven't? There seem to be multiple cases of choir practice reported as spreaders, but not the CPC run for instance.”

- No, the FACS model is currently too coarse-grained for that. To really identify superspreader events, you'll probably need data on the ventilation and cleaning regime in a given location and to more precisely figure out what people do in such a place (e.g., do they exercise, how much do they talk etc.).

About the Conversation review

“Is there a difference between [the generative model you've reviewed] and “agent-based” models?”

- Yes, very much so. This is a mean-field model, so it models probabilities over a population without resolving individual behaviors, while an agent-based model (usually) models individuals explicitly. An example of an agent-based model is the model used in Imperial Report 9, or the FACS model that we just wrote a paper about :).

Credits

Header image courtesy of the FACS paper.

It's a big gap, but GameWorld is back! (at least for now ;)).

Last time, we started with making plain tiles, as well as basic grid and brick structures. Today, I am going to extend this with 3+1 extras:

• Balls or spheres.
• 3-dimensional bricks.
• A basic tree
• ...and for the Coil subscribers a bonus tile drawing that I made together with my daughter ;).

We are using the same approach as last time (I do recommend doing that tutorial first), but extend it with a few new routines.

Pre-amble: adding shades and highlights

Because several of the shapes need shadows and highlights to give them a 3D look, we start of with making a simple function that creates shadow and highlight color, given a default starting color.

Here is the function to make a shading color, which we put in tile_patterns.py:

def shade(rgb, intensity=2):

tmp = [0,0,0]

for i in range(0, len(rgb)):

tmp[i] = int(rgb[i]/intensity)

return tmp[0],tmp[1],tmp[2]

Simply put, I define a shadow as a color with half of the values of the regular color. And for highlights, I do the opposite, which looks like this:

def highlight(rgb, intensity=2):

tmp = [0,0,0]

for i in range(0, len(rgb)):

tmp[i] = min(255, int(rgb[i]*intensity))

return tmp[0],tmp[1],tmp[2]

Making a (rudimentary) ball or sphere

Now, to make a sphere with highlight and shading, we first need to make a circle. This you can do as follows:

def draw_circle(t, i, color, xc, yc, xc2, yc2):

d,x,y,tw,th = t.get_properties(i)

d.ellipse([x+xc,y+yc,x+xc2,y+yc2],color)

In my simplistic tutorial, I simply make a ball by placing three circles at on top of each other, each with a size and a position that helps convey some depth. This looks as follows:

def draw_ball(t, i, hcolor, color, lcolor, xc, yc, xc2, yc2):

w = xc2-xc

h = yc2-yc

draw_circle(t, i, lcolor, xc, yc, xc2, yc2)

draw_circle(t, i, color, int(xc+w/20), int(yc+h/20), int(xc2-w/8), int(yc2-h/8))

draw_circle(t, i, hcolor, int(xc+w/7), int(yc+h/7), int(xc+w/2.5), int(yc+h/2.5))

Here, lcolor is the shadow color, which is used for the biggest background circle. I then put a slightly smaller circle on top of that, aligned to the top left, with the default color. Lastly, I add a small circle with the highlight color (hcolor) in the top left area of the main circle, to indicate a highlighted region. Combined, this will make a ball roughly like this:

Now, be aware that there are much better ways to do this, but I went straight for simplicity here.

Making a 3D rectangle

Similarly, we can add shading and highlights to rectangles. This we can do as follows:

def draw_3drect(t, i, color, x1, y1, w, h):

rgb = ImageColor.getrgb(color)

w -= 1

h -= 1

d,x,y,tw,th = t.get_properties(i)

We first decide on the size of the shaded and highlighted region, which corresponds to the depth of the rectangle. I chose a ratio of 0.1.

shade_size = 0.1

shade_width = max(1,int(shade_size*w))

shade_height = max(1,int(shade_size*h))

hl_size = 0.1

hl_width = max(1,int(hl_size*w))

hl_height = max(1,int(hl_size*h))

Next we draw the main rectangle (everything else will come on top of it)

draw_rect_hwrap(t, i, color, x1, y1, w, h)

And on the right side and the bottom side, two shaded rectangles:

draw_rect_hwrap(t, i, shade(rgb), (x1+w-shade_width)%tw, y1+hl_height, shade_width, h)

draw_rect_hwrap(t, i, shade(rgb), x1+hl_width, y1+h-shade_height, w-hl_width, shade_height)

Lastly, we draw two highlight rectangles on the left and on the top.

draw_rect_hwrap(t, i, highlight(rgb), x1, y1, hl_width, h-shade_height)

draw_rect_hwrap(t, i, highlight(rgb), x1, y1,w-shade_width, hl_height)

Note that I am using a function called “draw_rect_hwrap() here, which I am about to explain :).

Making 3D looking bricks

To make 3D bricks, we first need 3D rectangles representing each brick. But to make the pattern repeating, we also need those rectangles to wrap properly around the sides of the tile. To do this, we need a special version of draw_rect() which is used in the same way, but wraps around the sides. That one looks like this:

def draw_rect_hwrap(t, i, color, x1, y1, w, h):

d,x,y,tw,th = t.get_properties(i)

if x1+w>tw:

draw_rect(t, i, color, x1, y1, tw-x1, h)

draw_rect(t, i, color, 0, y1, x1+w-tw, h)

else:

draw_rect(t, i, color, x1, y1, w, h)

Now the next step, is to simply place the rectangles side by side, with alternating offsets so that we get a brick pattern. We do that like this:

def draw_3dbrick(t, i, color="#900", width=24, height=12):

d,x,y,tw,th = t.get_properties(i)

row = 0

b = 0

a = 0

while b < th:

while a < tw:

draw_3drect(t, i, "#A22", a, b, width, height)

a += width

b += height

row += 1

a = int(((width)/2) * (row%2))

..and once we do that, we can make a brick like this:

Making a tree

There are a *lot* of ways to make a tree, but a simple one is to simply use a brown stick, and put on it a pattern of green balls. Here's what that looks like in code:

def draw_tree(t, i, hcolor="#4f4", color="#0a0", lcolor="#060"):

d,x,y,tw,th = t.get_properties(i)

d.rectangle([x+20, y+24, x+28, y+48], "#660")

The next line contains all the coordinate pairs where we place the green spheres:

for xy in [[8,9],[18,4],[27,10],[6,19],[20,14],[28,10],[18,24],[28,19]]:

draw_ball(t, i, hcolor, color, lcolor, xy[0], xy[1], xy[0]+16, xy[1]+16)

And when you use this, you get a simple tree like this!

Closing thoughts

It's all very simple stuff still, but I think you get the idea: with each simple drawing function that combines existing drawing functions, we're able to add a little more variety and depth to our tile graphics.

I've added the Repl in the Appendix, and I extended the tile demonstrations, which now look like this:

And the functions to make the last 5 tiles are as follows in main.py:

tp.draw_circle(t, 12, "#DD3", 0, 0, 47, 47)

tp.draw_ball(t, 13, "#FF6","#DD3", "#AA2", 0, 0, 47, 47)

tp.draw_tree(t, 14, "#4f4","#0a0", "#060")

tp.draw_dog(t, 15)

tp.draw_3dbrick(t, 16, "#A22")

Who knows what we'll focus on next? Perhaps it's even more advanced tiles, or perhaps something entirely different....

Appendix 1: Full Repl.

You can find the online runnable Repl.it here: https://repl.it/@djgroen/Gameworld-10-Tile-Generator-II#tile_patterns.py

Lockdown has been lasting for a long time, and myths have filled the internet all over the place. Today I want to try and dispel a few of those myths, but also point out some things that are happening, but also very weird when you start thinking about them.

What is wrong

1. Trump's Covid-19 medicine (hydroxychloroquine) helps... and if it doesn't help it doesn't hurt.

I'm sorry everyone, but the results are in, and disprove this completely. Trump's medicine increases the chance of dying by a third on average, and also causes heart arrhythmia as a major complication in many patients. Many of Trump's statements are open for multiple interpretations, but in this case there is no ambiguity. He is taking the medication himself, and is a fool for doing so.

2. Most of us have been infected already

We can now also safely say that this one is wrong. Many groups have now tested for anti-bodies, and even in hard-hit states like France and Spain only 5% of people appear to have been infected: https://twitter.com/EricTopol/status/1260666412164542465

In *very* hard hit cities like New York, the percentage may be as high as 20%, but even that is only a small minority of the population.

A rough and incomplete overview of various tests can be found here: https://docs.google.com/spreadsheets/d/17Tf1Ln9VuE5ovpnhLRBJH-33L5KRaiB3NhvaiF3hWC0/edit#gid=0

3. We are accurately tracking the Covid-19 pandemic

Various websites like Worldometers and Ourworldindata give exact numbers on how many cases have been confirmed and how many deaths are confirmed. Meanwhile, the Financial Times is tracking how many more people are dying than normally around this time of year. Now, first of all all three of these sources are reporting very different numbers, with the Financial Times often reporting the highest numbers.

But the sad thing is that even the Financial Times is underestimating the deaths. For instance, let's look at the graph in that article today, on May 23rd:

The numbers look pretty dramatic here. For instance, the FT reports 8,900 excess deaths in the Netherlands, while Worldometers reports about 5,800 deaths from Covid-19.

But if you look even more closely, you'll find that the little excess death graph from the FT ends on... April 26th, almost a month ago.

Likewise, for the US it reports 52,300 deaths on April 18th, and on that same day Worldometers reported about 40,000 deaths. Today, worldometers is reporting about 98,000 deaths in the US, but given the previous discrepancy with the FT data, I would argue that 130,000 is probably a more realistic estimate.

To further compound this incredible mess, there are almost certainly countries out there that deliberately underreport their deaths.

4. Smoking reduces the risk of Covid-19

Yes, I fell for this one as well. But it doesn't stand up to serious scrutiny really.

What is weird

Having dispelled some myths, I now would like to cover a few things that are just plain weird; things we should be reconsidering.

1. Schools are closed, but after-school activities are continuing in full steam online

For two months now, my daughter is doing online zoom classes about ballet, singing, acting, and she even got offers to do online karate. Yet, when it comes to actual school, there are no such online streaming sessions, and pretty much the whole of the UK has to do with weekly homeschooling workload e-mails.

I understand that afterschool clubs provide online classes simply because they might go out of business otherwise (and schools do not), but isn't this whole situation getting a little bit ridiculous?

2. The obsession with the reproductive rate R appears ever lasting

As a reminder, the reproduction rate R is the average number of people that a given patient will infect on average. A number less than 1 indicates that, on average, an epidemic fizzles out, and a number greater than 1 indicates that it is growing.

I am not fundamentally against measuring epidemics in this way, but it is painful to see how R gets completely misused by just about everyone. Allow me to indulge on listing the sins.

1. Politicians are telling us that an R lower than one means we're doing well. There is a very simple counterpoint to make here: the easiest way to get a low R on the short term is to do far too little testing. And that is exactly what happened during this pandemic.

2. Modellers are putting R as an input parameters in their model, but also reporting R as an output. The Kucinskas code is just one example of it, but modellers are doing it just about anywhere. This can be dangerous, because it means that any error in your initial estimation of R immediately passes on as errors in your model outputs. Also, there is just something fundamentally weird about putting a measure as input and then producing it as an output, it feels a bit like second-serving food in a restaurant...

3. The community has cheerfully abandoned much simpler measures in favor of “R”

At the start of the pandemic, people still spoke about doubling times, or the percentage growth per day or week of the number of affected cases or deaths. All these measures are simpler and more intuitive than this R number. But some I suppose the magical “R” number makes for more appealing article titles?

3. The stock market just pretends nothing has happened

The S&P 500 is actually at a higher point than it was a year ago, even though 38 million people (and counting...) have been laid off:

S&P 500 index over the last year. From Google Search.

I cannot begin to fathom what warped logic drives this perception of the future business potential in the US.

Credits

Header image courtesy of Marco Verch.

Oh, and a last thing popped up for the subscribers:

Here's a small discovery I made while in self-isolation: drum tutorials!

A good friend of mine (Rob Pennel) is a professional drum teacher, and he has been sharing very minimalistic, but effective drumming tutorials for kids online. Because I think they're really cool and I have his permission to share them, I am going to post them here as they're very quick and effective (<5 minutes per lesson).

I enjoyed doing them with Eos, perhaps you find them fun too?

Lesson 1 – Simple rhythm

Lesson 2 – Simple phonics, 2:4 rhythm

Lesson 3 – Simple rhythm times

Lesson 4 – Simple phonics, 4:4 rhythm

Time will tell whether a fifth lesson will emerge :).