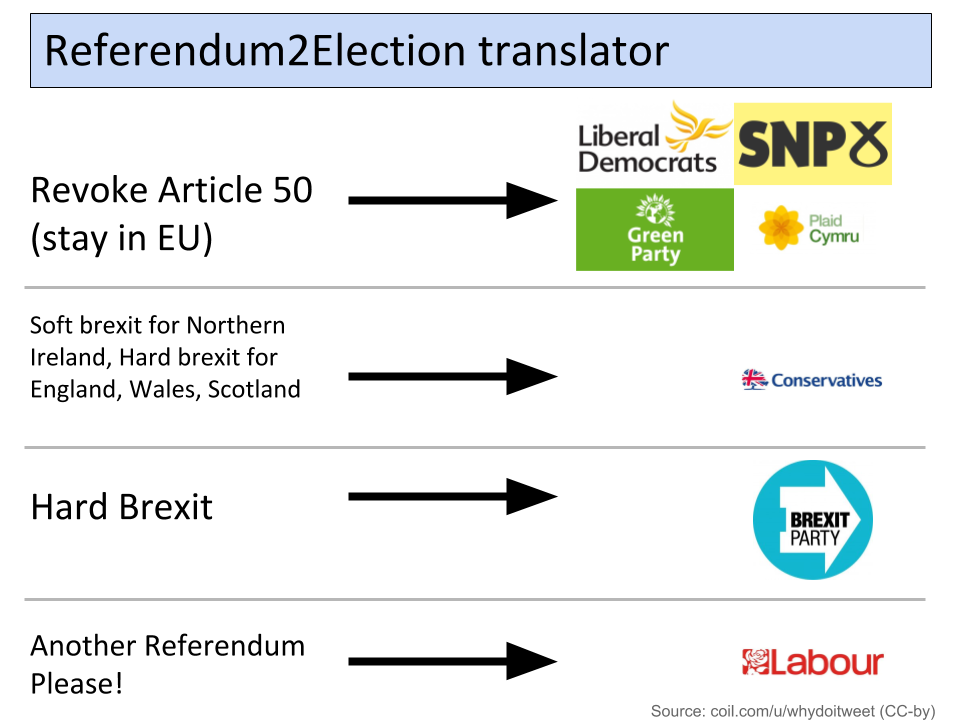
Small Sims 8: Simulating the vibration of a guitar string
Small Sims 8: Simulating the vibration of a guitar string
Today, in the spirit of xrpguitar, Steve Lukathar and many other guitar-enabled artists we are going to model a vibrating (guitar) string.
Sometimes I have to make simulations entirely from scratch, but this time I found an existing tutorial that actually helped me part of the way. In that post the author focuses mainly on the physics and not so much on the code, and the implementation with matplotlib is rather slow.
For this tutorial, I made a modified implementation that is (a) shorter, (b) in PyGame (so we can extend it later) and © a bit easier to adjust. I also plan to focus more on explaining the code, and a bit less on the pure physics.
The Physics part
Since the existing tutorial covers the physics side rather well, I'll keep the discussion brief here. Essentially we assume that the string is fixed on both ends (like with a guitar). To then make a model of it we use something called the wave equation, which combines a wave travelling to the left, and one to the right:

Here, x is the horizontal position and u(x,t) is the vertical position of a piece of guitar string in the simulation. Then there is a generic function for a wave travelling to the left (f(x-ct)) and for a wave travelling to the right (g(x+ct)).
In this tutorial, we use a specific version just to get something visible and cool. We will make both the left-travelling and right-travelling parts similar in magnitude, so that we have a standing wave:

Now all we have to do is to figure out what all these letters mean and should be, and resize the whole thing to fit our 800x600 screen, and then we're practically done! :)
Setting up the simulation
Unsurprisingly perhaps, we're going to use PyGame again. Why?
Because it performs well.
Because it's much easier to make more extended interactive simulations off a PyGame code than off a static pyplot.
And because it actually seems to lead to a more compact and elegant code (!)
Please see this tutorial to see how you can create a PyGame Repl, which is exactly what we need to do here now :).
The whole thing is a mere 31 lines of code (nice and compact, right?), and the first 10 lines you already get for free, as we need those to initialize PyGame (they've been the same in many of my tutorials):
import pygame
import time
import numpy as np
from numpy import pi
pygame.init()
width, height = 800, 600
backgroundColor = 0, 0, 0
screen = pygame.display.set_mode((width, height))
screen.fill(backgroundColor)
Okay, not totally the same, because we are importing numpy this time for calculating the sine values. In an ideal world we all know/recall exactly what the sine is, and no one will actually click that Wikipedia link, but then again we don't live in an ideal world and I for sure forgot a lot of my high school knowledge. We also
import the notion of pi (3.1415 etc...).
Slamming in the equation
Before we put in the equation itself, we need to define what the constant values in that equation (and in the simulation) should be, these are:
c = 1 # wave speed
dt = 0.1 # time increment
string_length = 4 # string length
You can tinker with the first two to get faster or slower moving strings, and with the third one to change the length (period) of your waves.
The wave equation example itself is a function u(x, t), and we can translate it directly into the Python code like this:
#Wave equation solution
def u(x,t):
return 0.5*(np.sin(x+c*t) + np.sin(x-c*t))
As you can see, it looks simple once you know and understand the equation it is derived from. However, if you don't understand the equation (e.g. you come across the code without having seen the equation), these mathematical notations can actually look a bit confusing...
The main loop
We're already half way now! So, before the main loop we need to initialize the timer,
t = 0
upon which we can start the main loop itself, which I made infinite.
while True:
We fill the screen with the black background color, to remove any previous string visualizations,
screen.fill(backgroundColor)
and then will calculate and render each of the 800 pixels of the string, one by one:
for sx in range(0, 800):
In this sub-loop we first have to rescale the screen x value (sx) from a scale of the screen length to a scale of a single string wave segment in our wave equation. We do this by multiplying it by the string_length*pi, and dividing it by the width of the screen in pixels:
x = ((float(sx) / 800.0) * float(string_length)*pi)
Next, we plot our pixel. The x coordinate is our screen x value (sx), but the y coordinate is a bit more intricate. It is initially the result of the converted x value (x) applied to our wave function (u(x, t)). After that we multiple the value by 600/pi to convert the scale back from the equation scale (height of pi) to the screen scale (which has a height of 600 pixels). We also add 300 pixels, so that any resting string (y=0) will be in the center of the screen. Lastly, we color the pixel white ((255, 255, 255)). Now that's a lot of stuff, but it all results in only one line of code that sets one pixel!
screen.set_at((sx, int(u(x, t)*600.0/pi + 300)), (255, 255, 255))
After we've done that for all 800 pixels, we simply increment our timer by dt (the time step size which we defined earlier on).
t += dt
Display the whole thing on the screen and sleep for 20 milliseconds!
pygame.display.flip()
time.sleep(20 / 1000)
Once you have all the code in, you should get an animation like this, but more smooth:

I just hand-stacked 4 frames together here, so apologies if it looks choppy ;).
Closing thoughts
This is certainly one of the easier tutorials I've created, but a vibrating string is such a quintessential simulation scenario, that I felt I just couldn't run a blog without it! Next time I'll try to do something quite different again!
Now all that's left is me sharing the source code and Repl. Also, for subscribers I'll signpost to a few more nice blog entries on other topics from the student (Mic) who made that initial tutorials, as they are quite hard to track down on his page. I might make an improved version of a few of those tutorials in due time, but definitely not all of them (some are far too niche for my liking).
(Back to Small Sims Index)
Credit
Header image courtesy of pxhere.com (CC0).
Appendix A: Source code and Repl
import pygame
import time
import numpy as np
from numpy import pi
pygame.init()
width, height = 800, 600
backgroundColor = 0, 0, 0
screen = pygame.display.set_mode((width, height))
screen.fill(backgroundColor)
# Original Source (with matplotlib): http://firsttimeprogrammer.blogspot.com/2015/07/the-wave-equation-2d-and-3d.html
c = 1 # wave speed
dt = 0.1 # time increment
string_length = 4 # string length
#Wave equation solution
def u(x,t):
return 0.5*(np.sin(x+c*t) + np.sin(x-c*t))
t = 0
while True:
screen.fill(backgroundColor)
for sx in range(0, 800):
x = ((float(sx) / 800.0) * float(string_length)*pi)
screen.set_at((sx, int(u(x, t)*600.0/pi + 300)), (255, 255, 255))
t += dt
pygame.display.flip()
time.sleep(20 / 1000)
And the Repl is available here.