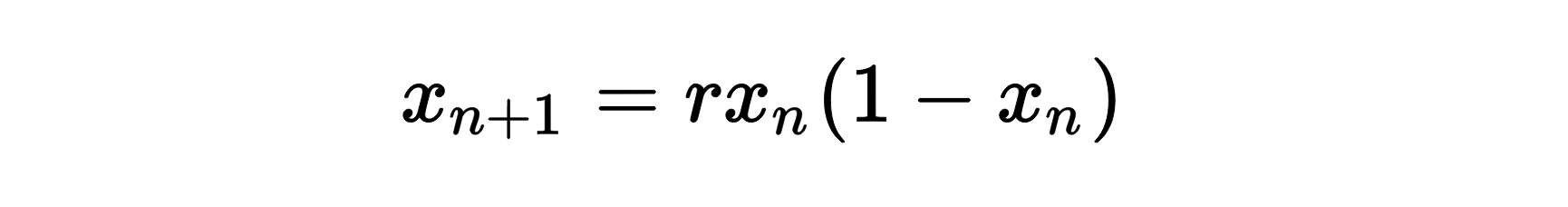viewRandom quotes 6
“the core building block of learning: the feedback loop. The value of this loop is captured in an equation: speed x clarity. Speed is how fast you iterate. Clarity is how well you extract signal from the noise” (Linda Z)
“the days are long, but the years are short” (Gretchen Rubin)… but especially as a parent !
“one day, I'll see my children grow up. They'll get married and pursue dreams. They won't need me anymore. I'll be so happy for them. But I will weep inside, as I see them walk across that stage, or drive to that airport, or walk down that aisle.” (Janie Porter)
“sur des plateformes comme Facebook ou Twitter, l’enjeu est d’occuper l’espace du débat plutôt que de construire un projet commun. Dans cet environnement, la gestion collaborative est plus compliquée à mettre en œuvre (que sur Wikipedia” (Romain Badouard)
“Sometimes you think people are stopping you from getting to the top and forget it's your mouth. Talk a bit less and do a bit more.”
“Que demandent les gens aux politiques ? De l'emploi et du pouvoir d'achat. Il ne faut pas attendre le changement d'en haut, mais d'en bas. Barbara Pompili a un boulot impossible, elle lutte contre le Graal de tout gouvernement : la croissance.” (Yann Arthus Bertrand)
“Il y a une nouvelle génération. Ils sont intelligents, ils lisent. Et quand on lit et qu’on est intelligent, aujourd’hui, on devient écolo.” (Cécile Duflot)
“It’s costly to have a team focused on the wrong metric.” (Gibson Biddle)
“As a product builder we can build anything, but we can't build everything” (Gibson Biddle)
“People hear what they want to hear. So as a PM you need to be super clear about what people should hear in what you say” (Gibson Biddle)
“Before you get all excited by the low-hanging fruit, be sure you are under the right tree” (Shreyas Doshi)
“Si hortum in bibliotheca habes, deerit nihil” (Cicero) – If you have a library overlooking a garden, you have everything you need
Other publication with random quotes , random quotes 2 , random quotes 3 , random quotes 4 , random quotes 5
viewRandom quotes 5
“Slow down at the start so you can move faster in the right direction”
(Sarah Kilian)
“The PM who thinks he knows his customer is like a male gynecologist” (Dave Mascha)
“To get ambitious stuff done, be short-term paranoid, long-term optimistic.” (Linda Zhang)
“The goal of a PM is not motion, it’s progress on solving customer problems better than anyone else” (Linda Zhang) (corollary : “I don't care if the dev team gets bored for 3 straight weeks”)
“No one ever made a decision because of a number. They need a story.” — (Daniel Kahneman)
“Only a fool learns from his own mistakes. The wise man learns from the mistake of others” (Otto von Bismarck)
“People and teams are consistently overly optimistic about the time it will take to complete a future task” (Daniel Kahneman)
“Scale is allergic to nuance.” (Jack Butcher)
“Leadership is solving problems. The day soldiers stop bringing you their problem is the day you have stopped leading them. They have either lost their confidence that you can help, or concluded you do not care. Either case is a failure of leadership” (Colin Powell)
“If we are confident that the change aligns with our product strategy and creates a better experience for users, we may forgo an A/B test.” (Des Navadeh)
“When making plans, think big. When making progress, think small.” (James Clear)
“It is remarkable how much long-term advantage people like us have gotten by trying to be consistently not stupid, instead of trying to be very intelligent.” (Charlie Munger)
“Violence is the last refuge of the incompetent.” (Isaac Asimov)
Other publication with random quotes , random quotes 2 , random quotes 3 , random quotes 4
viewChronique littéraire 14 (Keller & Papasan)
Gary Keller & Jay Papasan – The One Thing (Passez à l'essentiel)
I've started to get interested on the topic of Focus some time ago, and already wrote about it (see here or here). As a feedback, a colleague of mine asked if I had read The One Thing, which I didn't – but now it's done !
Focus comes in many different shape or form. G. Keller & J. Papasan boil it down to 1 question : What's the ONE thing I can do such that by doing it everything else will be easier or unnecessary?
The book covers 3 parts : 1/ false ideas that drives us away from the truth 2/ what is the simple path to productivity 3/ how this can unleash extraordinary results.
The book itself has a lot of examples, it's a pretty simple read. I'd say it falls in the 'inspirational, sometimes a bit bullshit, with interesting wisdom' category – and definitely lacks scientific support.
And as usual with “business” books, there is fluff and I guess it could be streamlined to a blog post (but no money or fame in that). So I will do it for you !
Nota : I read the book in french, so all quotes are in french
“quand on court deux lièvres à la fois, on n'en attrape aucun (proverbe russe)”
“Curly : vous savez ce que c'est le secret de la vie ?
Mitch : Non, c'est quoi ?
Curly : Ca [il tend l'index en l'air]
Mitch : Votre doigt ?
Curly : Une chose. Une seule chose. Vous vous occupez de ça, et tout le reste n'a aucune importance
Mitch : Super, mais c'est quoi, comme chose ?
Curly : Ca, c'est ce qu'il faut découvrir”
“quand vous voulez mettre toutes les chances de réussite de votre côté, quel que soit le domaine, votre approche devrait être toujours la même. Minimisez”
“les résultats extraordinaires découlent directement du nombre de choses que vous pouvez ignorer”
“faute d'une formule claire pour prendre nos décisions, nos priorités deviennent affaire de réflexe plutôt que de réflexion”
” quand tout paraît urgent et important, tout est égal”
“nous agissons [ndr : et planifions, et décidons] comme si nous avions de la volonté à volonté”
“Prenez garde à la façon dont vous interprétez le monde. Il est exactement comme cela (Erich Heller)”
“le bonheur apparaît sur le chemin de l'accomplissement”
“La solution ? bloquer du temps”
“les quatre voleurs de productivité sont 1) l'incapacité de dire 'non' 2) la peur du chaos 3) la mauvaise hygiène de vie 4) un environnement qui ne soutient pas vos objectifs”
“le moindre 'oui' doit être défendu par un millier de 'non' “
“Deux ans après son retour [celui de Steve Jobs] en 1997, la gamme Apple passa de 350 à 10 produits.”
“les quatre [regrets] les plus courants [des personnes en fin de vie] sont : j'aurais aimé travailler moins, j'aurais aimé avoir le courage d'exprimer mes sentiments, j'aurais aimé garder le contact avec mes amis, j'aurais aimé m'autoriser à être plus heureux”
Other publication with similar content
viewPowerful presentations
I recently published a new article on Medium:
Making powerful presentations : back to basics
This covers what makes a presentation powerful, and the key steps to follow to make sure yours will be, too.
Quote : “Good slides are an essential tool to master to have an effective communication.”
Happy to get your feedback on it :)
Other publication with Medium articles
viewRandom quotes 4
“Everybody at every level should have an equal voice in the outcome, based on the strength of his or her arguments.” / “If we have data, let’s look at the data. If all we have are opinions, let’s go with mine.” (James Barksdale)
“Les êtres passionnés par une seule idée me fascinent, car plus quelqu'un se limite, plus il s'approche en réalité de l'infini. Ces gens-là, qui semblent s'écarter du monde, bâtissent avec leur matériau particulier un univers en miniature.” (Stephan Zweig)
How can I show this (vs. tell) with the least number of graphs possible?
Trace the genealogy of your ideas
“Success can usually be measured by the number of uncomfortable conversations we are willing to have and the number of uncomfortable actions we are willing to take.” (Tim Ferriss)
“You never change things by fighting the existing reality.
To change something, build a new model that makes the existing model obsolete.” (Buckminster Fuller)
“You never rise to the level of your vision. You fall to the level of your decision-making.” (Shreyas Doshi)
“Tout Homme qui dirige, qui fait quelque chose, a contre lui, ceux qui voudrait faire la même chose, ceux qui font précisément le contraire, et surtout la grande armée des gens, beaucoup plus sévères, qui ne font rien.” (Jules Claretie)
“Ultimately, what a product manager has to constantly fight is ambiguity” (Ken Morton)
There are 4 types of wealth: 1. financial wealth (money) | 2. social wealth (status) | 3. time wealth (freedom) | 4. physical wealth (health)
be wary of a job that lure you in with 1 and 2 but robs you with 3 and 4.
“Run towards trouble. It will say a lot about your maturity and character.” (Shreyas Doshi)
“Pan metron ariston” (παν μέτρον άριστον) : “everything in moderation”. (Quote in ancient Greek coined by Kleovoulos o Lindios in the 6th century B.C.)
Other publication with random quotes , random quotes 2 , random quotes 3
viewRandom quotes 3
“On ne construit pas un pont en comptant le nombre de personne qui traversent la rivière à la nage” (Brent Toderian)
“To see the world, things dangerous to come to, to see behind walls, to draw closer, to find each other and to feel. That is the purpose of life.” (James Thurber)
“C’est une intarissable source d’inspiration quand il s’agit d’aider quelqu’un à avancer, car je sais qu’il n’y a pas besoin de savoir où il compte aller, ni comment il va faire. Il suffit parfois d’être là, d’être attentif, d’être admiratif, de ne pas avoir peur de jeter une pincée d’absurde dans l’arène. Et d’oublier que l’on ne sait pas.” (Rémi Guyot)
“Beautiful things don't call for attention” (James Thurber)
“The reality is that we have zero years [to address Climate change] and we have to change all of our infrastructure.” (Saul Griffith)
“When you're the janitor, reasons matter. Somewhere between the janitor and the CEO, reasons stop mattering. That Rubicon is crossed when you become VP” (Steve Jobs)
“Le génie de cette voiture réside dans ses renoncements.” (Jean Savary en parlant de la Citroen Ami)
” Un product manager doit non seulement prendre les bonnes décisions, mais aussi minimiser le coût nécessaire à la prise de ces décisions. En particulier, protéger le temps des autres équipes sollicitées pour informer ces décisions.” (Remi Guyot)
“the first kid is very hard to handle. the second makes you recognize how easy only one kid was. the third is raised by the first two, and the forth is raised by themselves.”
“une solution qui vous démolit vaut mieux que n’importe quelle incertitude” (Boris Vian)
“Those who make peaceful revolution impossible, make violent revolution inevitable” (John f. Kennedy)
Other publication with random quotes , random quotes 2
viewBeauty in formulas
It's everywhere.
Formula for 3, by Ramanujan :
 Euler's formula :
Euler's formula :

The logistic map :
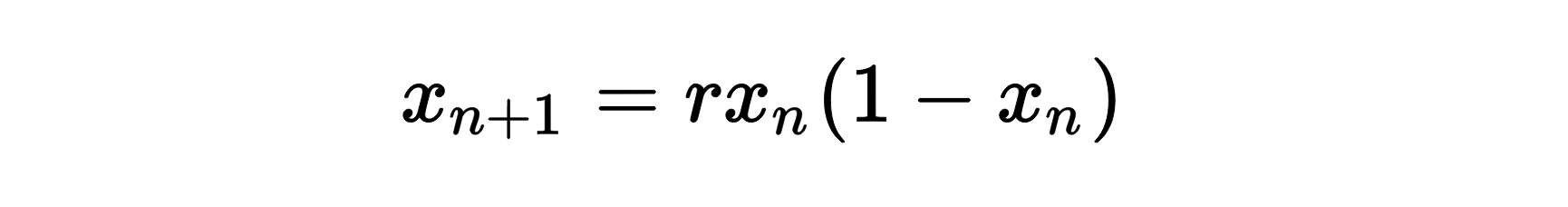
The Classical wave equation :

Other publication on mathematics Riemann hypothesis – a tentative at making it accessible
viewChronique littéraire 13 (Ariely)
Dan Ariely – Predictably Irrational
Another book about behavioural economics & psychology... Although there are some similarities between Thinking, Fast & Slow, in Predictably Irrational, Dan has kept the topics brief and discussions to the point with very few experiments/studies. The interest is hence better sustained, and the read easier. The premise of the book is that human beings make consistently irrational decisions. The author tries to uncover the root causes, and effects of these behaviors. For instance, he shows the huge difference there is between “almost free” and “free”; he explores the 2 norms that we live by all the times : social vs. market; he explains how and why ownership distorts the perception of value...
A must-read for product managers, marketers, and everyone that can benefit from knowing more about sociology !
“humans rarely choose things in absolute terms. We don't have an internal value meter that tells how much things are worth. Rather, we focus on the relative advantage of one thing over another, and estimate value accordingly”
“Most people don't know what they want until they see in context”
“we find it easy to spend $3,000 to upgrade to leather seats when we buy a new $25,000 car, but difficult to spend the same amount on a new leather sofa”
“The more we have, the more we want. And the only cure is to break the cycle of relativity”
“Herding : When we assume something is good or bad on the basis of other people's previous behavior, and our own action follow suit. But there is also another kind of herding, one that we call self-herding. This happens when we believe something is good (or bad) on the basis of our own previous behavior.”
“Why do we have an irrational urge to jump for a FREE! item, even when it's not what we really want ? I believe the answer is this. Most transactions have an upside and a downside, but when something is FREE! we forget the downside. FREE! gives us such an emotional charge that we perceive what is being offered as immensely more valuable that it really is. Why ? I think it's because humans are intrinsically afraid of loss”
“Money is very often the most expensive way to motivate people”
“Life with fewer market norms and more social norms would be more satisfying, creative, and fun”
“When prices are zero and social norms are part of the equation, people look at the world as a communal good. [...] Not mentioning prices ushers in social norms, and with those social norms, we start caring more about others”
“we are in love with what we already have”
“Our aversion to loss is a strong emotion, [...] one that sometimes causes us to make bad decisions. [...] we often refuse to sell some of our cherished clutter, and if somebody offers to buy it, we attach an exorbitant price tag to it”
“In 210 BC, a chinese commander named Xiang Yu led his troops across the Yangtze river to attack the armi of the Qin dynasty. Passing on the banks of the river for the night, his troops awakened in the morning to find, to their horror, that their ships were burning. They hurried to their feet to fight off the attackers, but soon discovered that it was Xiang Yu himself who had set their ships on fire, and that he had also ordered all the cooking pots crushed. Xiang Yu explained to his troops that without the pots and the ships, they had no other choice but fight their way to victory or perish. That did not earn Xiang Yu a place on the Chinese army's list of favorite commanders, but it did have a tremendous focusing effect on his troops: grabbing their lances and bows, they charged ferociously against the enemy and won nine consecutive battles, completely obliterating the main-force units of the Win dynasty”
“What we need is to consciously start closing some doors.”
“Why are we so frequently dishonest ? This is my take. We care about honesty and we want to be honest. The problem is that our honesty monitor is active only when we contemplate big transgresssions, like grabbing an entire box of pens from the conference hall. For little transgressions, like taking a single pen or two pens, we don't even consider how these actions would reflect on our honesty and so our superego stays asleep.”
“Individuals who had mastered [...] knowledge, it was said, not only had a monopoly of practice of that knowledge, but had an obligation to user their power wisely and honestly. The oath – spoken and often written – was a reminder to practitionners to regulate their own behavior. “
viewFocus
I published a 2-parts story on Focus :
Focus : the Beauty of Theory
This part explains why Focus is so important, and why, in theory it shouldn't be too difficult.
Quote : “Managing too many topics in parallel is biologically unnatural and counterproductive.”
Focus : the Beast of Practice
This part explores why it's so difficult to achieve focus in reality, and suggests concrete methods to get better at it.
Quote : “Today, everything is presented as an opportunity, and distractions are everywhere.”
Happy to get your feedback on it :)
viewAbout
Hey!
I'm Nico, Senior Product Manager at BlaBlaCar, former consultant and engineer.
I'm father of 2, currently living in Paris, and passionate about Product management, science, environment... My curiosity leads me to some unusual places sometimes !
You can follow me on Twitter : @NicoBeytout
 Euler's formula :
Euler's formula :